Predictably Misbehaving
Lecture 4: Choice Over Time
Joshua Foster at UW-Oshkosh

Choice Over Time
Many economic choices involve tradeoffs over time.
Simple example: learning a new instrument.
- Costly money outlay at the beginning ($\downarrow$ utility)
- Pain and frustration of learning it ($\downarrow$ utility)
- Mastery ($\uparrow$ utility)
Key economic examples: savings/investment, education, health.
- Timing of $\uparrow$/$\downarrow$ utility introduces mistakes.
A Quick History
Four stages in the theory of intertemporal choice:
- Senior and Jevons (late 1800's): emotions are a large part of decisions involving time.
- Bohm-Bawerk and Fisher (early 1900's): cognitive issue - a tradeoff between today's satisfaction and tomorrow's satisfaction.
- Samuelson et al. (mid 1900's): removed psychological content for simplicity.
- Thaler et al. (late 1900's): A re-emergence of the influence of psychology on intertemporal choice.
Exponential Discounting
Traditional economics
Samuelson's discounted utility model.
Individuals choose the consumption bundle at each point in time $t$, $(c_t,c_{t+1},...,c_T)$, to maximize: \begin{equation*} U = u(c_t) + \delta u(c_{t+1}) + \delta^2u(c_{t+2}) + \delta^3u(c_{t+3}) + ... \end{equation*} where $\delta$ (usually $\leq 1$) is the discount factor.- Measures how consumption is valued across time.
- Interpretation: consumption next time step is always worth $\delta$ as much as the consumption now.
Example: utility from 100 bucks every day
Assume $u(100)=100$ and $\delta=0.9$
\begin{equation*} U = u(c_t) + \delta u(c_{t+1}) + \delta^2u(c_{t+2}) + \delta^3u(c_{t+3}) + ... \end{equation*}Then \begin{equation*} U = 100 + 0.9\cdot 100 + 0.9^2\cdot 100 + 0.9^3\cdot 100\; + ... \end{equation*}
Or \begin{equation*} U = 100 + 90 + 81 + 72.9\; + ... \end{equation*}
Dynamic Consistency
A truly magnificent property.
The action a person thinks they should take in the future always coincides with the action that they actually prefer once the time comes.
Examples:
- If today we wish ourselves to work on a problem set tomorrow, then tomorrow we prefer to work on the problem set immediately.
- If today we prefer to quit smoking tomorrow, then tomorrow we prefer to quit smoking immediately.
- If today we prefer to diet tomorrow, tomorrow we will want to diet immediately.
Marshmallow Example
On Day 0 a child has to decide between eating one marshmallow in Day 1 or two marshmallows in Day 2.Their consumption utility for marshmallows in each period is:
| u(no marshmallows) | = | 0 |
| u(1 marshmallow) | = | 20 |
| u(2 marshmallows) | = | 30 |
| u(no marshmallows) | = | 0 |
| u(1 marshmallow) | = | 20 |
| u(2 marshmallows) | = | 30 |
Let $\delta = 0.9$. Then:
For "reasonable" discount rates, child will prefer to wait for two marshmallows.
Now it is Day 1
On Day 1 a child has to decide between eating one marshmallow in Day 1 or two marshmallows in Day 2.Their consumption utility for marshmallows in each period is:
| u(no marshmallows) | = | 0 |
| u(1 marshmallow) | = | 20 |
| u(2 marshmallows) | = | 30 |
| u(no marshmallows) | = | 0 |
| u(1 marshmallow) | = | 20 |
| u(2 marshmallows) | = | 30 |
$U = u(c_1) + \delta u(c_2)$
Let $\delta = 0.9$. Then:
Despite the immediate temptation, the child will still prefer to wait for two marshmallows.

Conclusions of
Dynamic Consistency
Dynamic consistency implies:
- People form lifetime consumption plans, and execute them.
- People should have no regrets about smoking.over-eating.being in debt.dropping out of school.
- They have optimally weighed the benefits and costs of their actions.
Policy implications of dynamic consistency
Drug addicts optimally chose their
plan for themselves.
We should not try and interfere.
We will only make them less happy.
In actuality, people have a strong tendency to over-value immediate gratification,
Relative to their own long-term preferences.
- If so, then dynamic consistency no longer holds.
Samuelson: his functional form was arbitrary.
- He chose it purely for mathematical convenience.
"It is completely arbitrary to assume that the individual behaves so as to maximize an integral of the form envisaged."- Samuelson (1937) A Note on Measurement of Utility
In some sense, dynamic consistency was a revolution.
- It clarified a lot of the issues and simplified analysis.
- But also distilled the psychology into a variable, $\delta$.
Progress Report
Evidence from Frederick et al. (2002):
If you (economists) insist, what is $\delta$, then?
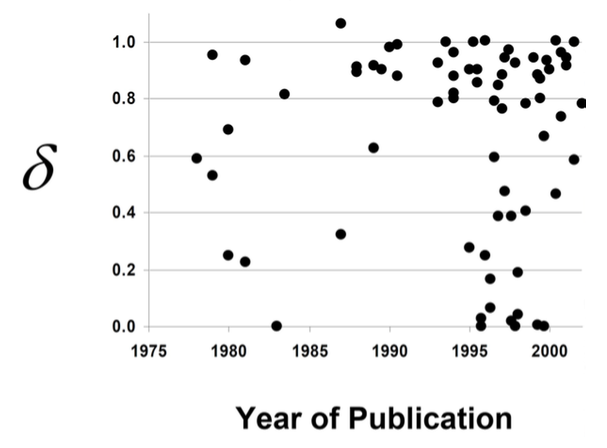
Economists have no idea what it is!
Short-run Vs. Long-run Goals
Short-run Impatience
Reality: People are very impatient in the short run."Suppose I could give you:
- 100 in cash right now, or
- X in cash in two weeks.
What is the smallest amount of money, X, I could offer you in two weeks to make you forgo the 100 right now?"
$\overline{X}=164$
Lots of people borrow on payday loans
- Pay up to 7000% annualized compounded interest.
- $40 billion industry
- More locations than McD's and Starbucks combined.



Short-run Impatience
Payday effect:
Consumption of various forms follows the pay cycle.
That is, people buy steaks, cigarettes, and alcohol on their payday, and struggle to coast through the end of the month.
- Shapiro (2005): the caloric intake of food-stamp recipients declines 13-14% over the food-stamp cycle.
- Huffman and Barenstein (2005): the expenditure of working households in the UK is 12% lower the week before payday compared to the week after.
Mathematical Argument
This is evidence on choices over immediate consumption.
What happens to similar tradeoffs further in the future?
Example from survey
On average...
- 100 dollars now $\sim$ 164 dollars in two weeks.
- To wait two weeks, must be paid $\frac{164}{100}$ times more.
If applied to an additional two weeks:
100 now $\sim\frac{164}{100}\cdot 164\approx 269$ in four weeks.If applied to a year delay:
100 now $\sim\left(\frac{164}{100}\right)^{26}\cdot 100\approx 38.5$M in a year.If applied to a two year delay:
100 now $\sim\left(\frac{164}{100}\right)^{52}\cdot 100\approx 1.5$T in two years.Very Small Discount Rates
Let's take a very small discount rate
100 today $\sim$ 101 tomorrow
- To wait one day, must be paid $\frac{101}{100}$ times more.
If applied to the next day:
100 now $\sim\frac{101}{100}\cdot 101=102.01$ in two days.If applied recursively for a year:
100 now $\sim\left(\frac{101}{100}\right)^{365}\cdot 100\approx 617,487$ in a year.If applied to a two year delay:
Indifferent between 100 now and 1T in two years.Also means indifferent between
- 100 in 10 years and 143,000 in 12 years.
Long-run Patience
"Suppose I could give you:
- 100 in cash in eight weeks, or
- X in cash in ten weeks.
What is the smallest amount of money, X, I could offer you in ten weeks to make you forgo the 100 in eight weeks?"
$\overline{X}=122$
Long-run Patience - from Thaler (1981)
"What $x$ makes you indifferent between $y$ today and $x$ in $z$ time?" $\rightarrow\delta$.
| $y$ | $z$ | Median $x$ | Discount factor $\delta$ |
| 15 | 1 month | 20 | 0.032 |
| 15 | 10 years | 100 | 0.83 |
| 40 | 6 months | 50 | 0.64 |
| 40 | 4 years | 90 | 0.82 |
The discount factor is increasing in the time delay, indicating subjects were more patient in the long run.
Discount Factors and Time
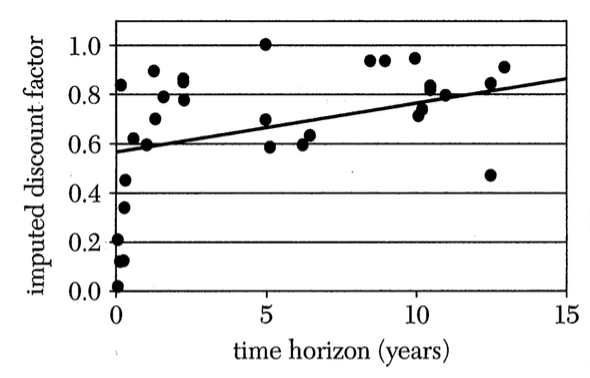
Back to Frederick, Loewenstein and O'Donoghue (2002)
In the real world...behavior is not consistent with exponential discounting, which claims the discount rate is always the same.
Intrapersonal Conflicts
One ancient and two modern examples...
Ulysses and the Sirens:
"These nymphs had the power...of charming by their song all who heard them, so that mariners were impelled to cast themselves into the sea to destruction. Circe directed Ulysses to stop the ears of his sailors with wax, so that they should not hear the strain; to have himself bound to the mast, and to enjoin his people, whatever he might say or do, by no means to release him till they should have passed the Sirens' island."
Financial advice:
"Cut up your credit and store cards! If possible get rid of all of your credit cards...Put temptation out of reach. If you really can't do without a credit card, limit yourself to only one. Put it in a tub of water and stick it in the freezer. Extreme? Maybe, but it will make you think hard about any impulse purchases you make in the future while you are standing there waiting for it to defrost."
Anonymous teacher evaluation:
"The problem sets should have been graded. I had no incentive to do them, and as a result did poorly on the exams."
Hyperbolic Discounting
Hyperbolic Discounting
Let's modify utility to take into account:
- People heavily discount the near future.
- People don't discount much in the 'further' future.
Start with exponential discounting:
\begin{equation*} u_t + \delta u_{t+1} + \delta^2 u_{t+2} + \delta^3 u_{t+3} + ... \end{equation*}But add a short-term discount factor $\beta < 1$.
\begin{equation*} u_t + \beta\left[\delta u_{t+1} + \delta^2 u_{t+2} + \delta^3 u_{t+3} + ...\right] \end{equation*}Purpose: $\beta$ underweights all future periods.
Example: suppose $\beta=\frac{1}{2}$ and $\delta=0.9$.
One marshmallow at $t=1$...or two at $t=2$?
| u(no marshmallows) | = | 0 |
| u(1 marshmallow) | = | 20 |
| u(2 marshmallows) | = | 30 |
Decision at $t=0$: Waits for 2!
Example: suppose $\beta=\frac{1}{2}$ and $\delta=0.9$.
One marshmallow at $t=1$...or two at $t=2$?
| u(no marshmallows) | = | 0 |
| u(1 marshmallow) | = | 20 |
| u(2 marshmallows) | = | 30 |
Decision at $t=1$: Take 1 now!
Major Takeaway
We smoke more, eat more, and work less tomorrow than today we wish our tomorrow selves to do.
Multiple Selves Approach

A student has three nights to complete a problem set
| Dates: | $t = 0$ | $t = 1$ | $t = 2$ |
| Utility: | $u_0=-1$ | $u_1=-\frac{3}{2}$ | $u_2=-\frac{5}{2}$ |
| Assume: | $\beta=\frac{1}{2}$ | and | $\delta=1$ |
What will this student elect to do at time $t=0$?
Utility of completing the problem set on $t=0$: $-1$
Utility of completing the problem set on $t=1$: $-\frac{3}{4}$
Utility of completing the problem set on $t=2$: $-\frac{5}{4}$
"I'll do it tomorrow night..."
A student has three nights to complete a problem set
| Dates: | $t = 0$ | $t = 1$ | $t = 2$ |
| Utility: | $u_0=-1$ | $u_1=-\frac{3}{2}$ | $u_2=-\frac{5}{2}$ |
| Assume: | $\beta=\frac{1}{2}$ | and | $\delta=1$ |
What will this student elect to do at time $t=1$?
Utility of completing the problem set on $t=1$: $-\frac{3}{2}$
Utility of completing the problem set on $t=2$: $-\frac{5}{4}$
"I'll do it tomorrow night..."