9483
AiS
Session 1b


Joshua
Foster

Agenda
- Quick Case: Pricing a Drink for Value Creation.
- Marginal Analysis for Profit Maximization.
- Maximum Price Heuristic.
Economist's objective: maximize profit.
- How do economists measure profit?
- How does this measure differ from "accounting" profit?
Profit $=$ Revenue $-$ Cost
- Where does revenue come from?
- Where do economists get this information?
- Where do costs come from?
- Where do economists organize this information?
Pricing a Drink for Value Creation
- The scenario involves RightPrice, a major supermarket in Africa, contemplating selling PRIME Hydration Drink.
- The drink, popular among children and influenced by social media, is available for purchase at a lower wholesale price.
- The case discusses potential pricing strategies and marketing considerations.
Objectives
- Value Assessment: Determine the potential value this product could add to the store's portfolio.
- Pricing Strategy Considerations: Identify key factors to consider in developing a pricing strategy for the drink.
| Group 1 | May El Damatty | Maro Egbedi | Zachary Zarnett-Klein | Judith Osemeke | Iain Smith | Akber Amanulla Khan | |
| Group 2 | Olamide Adeboboye | Sean Morris | Rutuja Desai | Kiera Treloar | Awaad Aamir | Valentina Efionayi | |
| Group 3 | Angelita Martin | Ishi Khamesra | Aliya Nazeer | Calvin Zehr | Olayinka Adesanya | Ishani Adityan | |
| Group 4 | Robert Gray | Sifan Wang | Rio Baudisch-McCabe | Sam Jain | Ella Smylie | Princess Adeniran | |
| Group 5 | Avneet Chohan | Mac Astritis | Sebastian Henao | Sam Macy | Gauri Angrish | Derek Adam | |
| Group 6 | Samira Jain | Elisabeth Iannucci | Kendall Zhang | Adam Meadows | Bella Natasha Diego | Silvia Pacheco Diaz | Chaitanya Gandhi |
Small Group Task
In your assigned groups, take the next 15 minutes to read the quick case and reflect on the questions it asks.
Be prepared to discuss your responses to these questions when time is up.
How does PRIME Hydration create value internally and externally for RightPrice?
What are the potential pros and cons of selling the drink?
| Pros | Cons |
| 1) | 1) |
| 2) | 2) |
| 3) | 3) |
What price do you set and why?
Optimal pricing with marginal analysis.
Select the price for which marginal revenue equals marginal cost ($MR=MC$).
- That is, select the price at which the money coming into the firm on the last unit is exactly equal to the money leaving the firm on said unit.
This rule is a workhorse for all of microeconomics.
| Demand | Revenue Information | Cost Information | Profit | |||
|---|---|---|---|---|---|---|
| Price | Quantity | Revenue | Marginal Revenue | Cost | Marginal Cost | Revenue - Cost |
| 6 | 0 | $6\cdot 0 = 0$ | $-$ | 0 | $-$ | 0 |
| 5 | 1 | $5\cdot 1 = 5$ | $\frac{5-0}{1-0}=5$ | 1 | $\frac{1-0}{1-0}=1$ | 4 |
| 4 | 2 | $4\cdot 2 = 8$ | $\frac{8-5}{2-1}=3$ | 4 | $\frac{4-1}{2-1}=3$ | 4 |
| 3 | 3 | $3\cdot 3 = 9$ | $\frac{9-8}{3-2}=1$ | 8 | $\frac{8-4}{3-2}=4$ | 1 |
| 2 | 4 | $2\cdot 4 = 8$ | $\frac{8-9}{4-3}=-1$ | 13 | $\frac{13-8}{4-3}=5$ | -5 |
| 1 | 5 | $1\cdot 5 = 5$ | $\frac{5-8}{5-4}=-3$ | 19 | $\frac{19-13}{5-4}=6$ | -14 |
Marginal Revenue: $MR=\frac{\Delta \text{Revenue}}{\Delta \text{Quantity}}$ and Marginal Cost: $MC=\frac{\Delta \text{Cost}}{\Delta \text{Quantity}}$
What makes applying marginal analysis difficult?
Maximum Price Heuristic.$^\dagger$
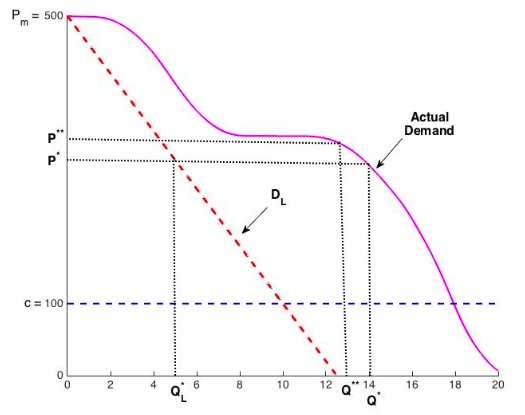
Select the price according to $P^*=(P_{\text{max}}+MC)/2$.
- $P_{\text{max}}$ is the maximum price that still sells a few units.
- $MC$ is the per-unit production cost (i.e. marginal cost).
$^\dagger$See Cohen et al. (2021) in Management Science for details.
Cohen et al. (2021), Figure 1.
Cohen et al. (2021), Figure 5.
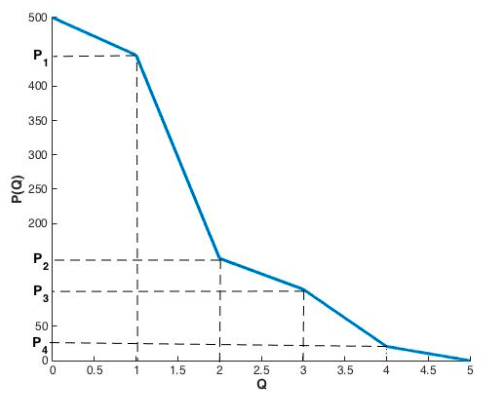
Among 100,000 simulations, this method assigned a price within 13% of the optimal profit over 80% of the time.
A few assumptions underlie this approach.
- The firm can estimate the maximum price, $P_{\text{max}}$.
- Marginal cost ($MC$) is known and constant.
- The firm need not know the quantity it will sell.
Would you apply this pricing heuristic to PRIME Hydration?
$P^*=(P_{\text{max}}+MC)/2$
$P^*=(42.48+1.59)/2=22.04$ (in USD)
Key takeaways.
- Demand curves give us information about where revenues come from and supply curves summarize our information about costs.
- A residual demand curve is the object that captures the number of units a firm will sell at each possible price, given the strategies of their competitors.
- Profit is maximized when a firm sets prices such that marginal revenue equals marginal cost ($MR=MC$).
- A useful alternative to marginal analysis is the Maximum Price Heuristic, which requires far less information.