Auctions for Risk Averse Charities
Joshua Foster at Ivey
Jeffrey Carpenter & Peter Matthews
at Middlebury College

Your favorite non-profit needs $\$$10,000.
Donor Community

50% chance @ 10k
50% chance @ 12k
New Wealthy Donor

10% chance @ 150k
90% chance @ 0
Your favorite non-profit needs $\$$10,000.
Winner-pay Auctions

50% chance @ 10k
50% chance @ 12k
All-pay Auctions

10% chance @ 150k
90% chance @ 0
Valuations
Bids
Revenues

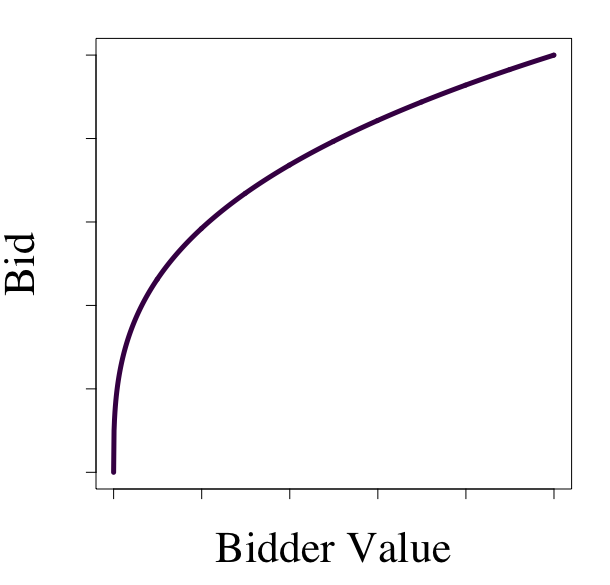
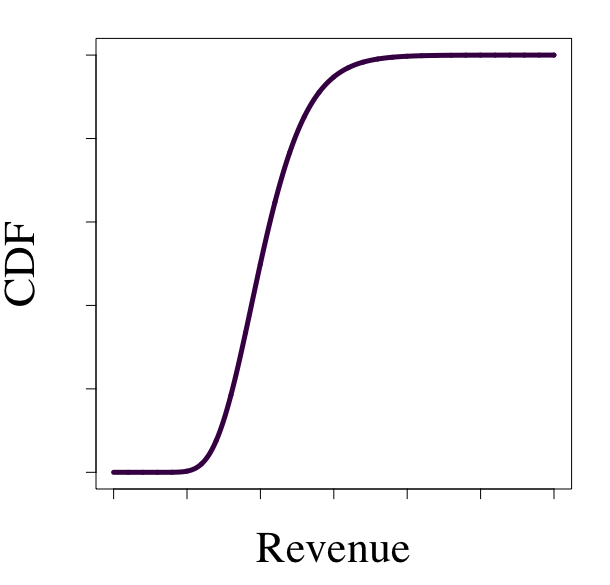
Our focus.
- Is there a theoretical/experimental mean-variance tradeoff among fundraising mechanisms?
- How might this be a function of participation costs?
- What advice can we give on fundraising design?
Experimental Design Overview
Tested 10 mechanisms with 5 sessions each.
10 potential bidders and 10 auctions per session.
Public good benefits imposed on auction revenue.
Phase 1: Earn Money
- 16 incentivized anagram puzzles.
- Difficulty exogenously varied.
Phase 2: Bid or Anagram
- Participate in an auction.
- Attempt another anagram (of known difficulty).
Imposed Mechanisms
First-price Winner-pay
Sealed bid, Dutch
Second-price Winner-pay
Sealed bid, English, Silent
First-price
All-pay
Sealed bid
Second-price All-pay
All-pay Button, "Bucket"
Last-price
All-pay
Sealed bid
Standard Lottery
Raffle
Standard IPV Framework
Expected ex ante bid $\overline{b}_m$ through mechanism $m$:
$\overline{b}_m=\int_{\hat{v}_m}^{\overline{v}}b_m(v)dF_m(v)$
With $n$ bidders, expected revenue is $\mu_m=n\overline{b}_m$.
Bidder's revenue variance:
$\text{Var}(b_m)=\int_{\hat{v}_m}^{\overline{v}}b_m(v)^2dF_m(v)-\overline{b}_m^2$
Variance $\sigma_m$ of mechanism $m$:
$\sigma_m^2=\text{Var}\left(\sum_{i=1}^n b_m^i\right)$
$=\sum_{i=1}^n\text{Var}(b_m^i)+2\sum_{i\leq j}\text{Cov}(b_m^i,b_m^j)$
Endogenous Participation
The $n$ potential bidders face a cost $c$ for participation.
- Motivation: bid preparation, fairness, etc.
- Experiment: expected value of an anagram puzzle.
- Upshot: active bidders is not pre-determined.
There exists a mechanism-specific fixed threshold value $\hat{v}$ that determines participation.
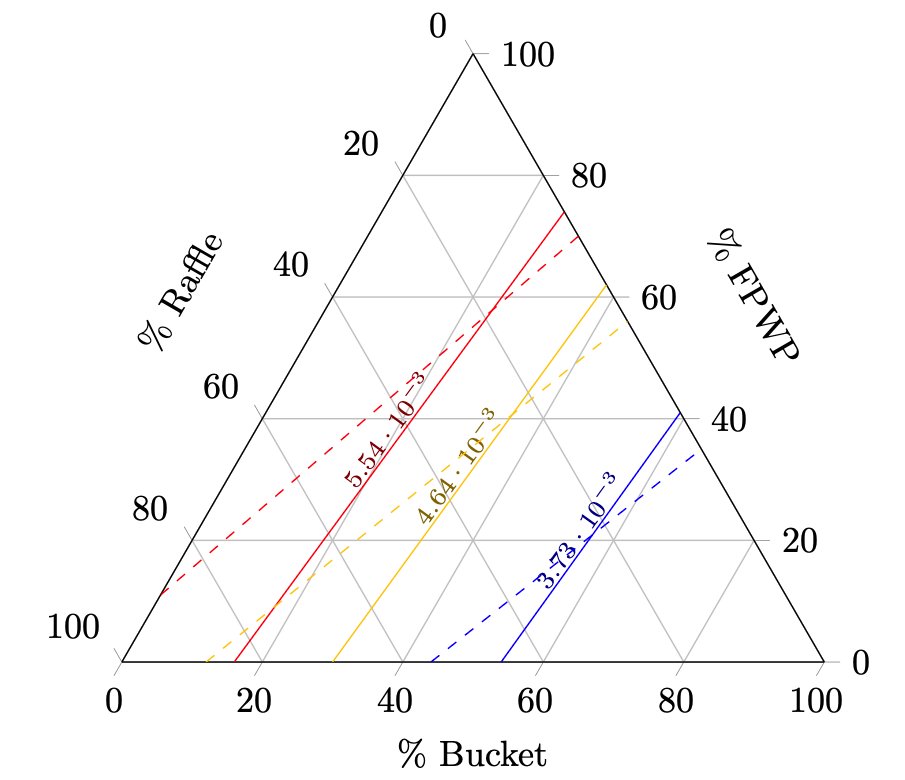
Theoretical Mean-variance Tradeoff by Mechanism, Participation Cost

Theoretical Mean-variance Tradeoff by Mechanism, Participation Cost

Prediction 1: Mechanisms with greater expected revenue also have greater variance.
Theoretical Mean-variance Tradeoff by Mechanism, Participation Cost

Prediction 2: Winner-pay variance will increase with participation cost, while all-pay variance will decrease.


Result 1: Nearly all mechanisms with greater expected revenue also have greater variance.
Participation & Revenue Variance by Puzzle Difficulty (OLS)

Participation & Revenue Variance by Puzzle Difficulty (OLS)

Result 2: An $\uparrow$ participation costs $\Rightarrow$ revenue variance to $\uparrow$ if winner-pay, but $\downarrow$ if all-pay.
Fundraising design: a "balanced" event.